AMPLIFICADORES DE INSTRUMENTACIÓN
Los amplificadores de instrumentación son amplificadores diferenciales con un CMRR alto, muchos de ellos con ganancia variable. En pocas palabras diremos que son amplificadores diferenciales buenos.
La primera cuestión a tratar sería el por qué debe ser un amplificador diferencial. Tiene muchas respuestas, la primera de ellas quizás sea el hecho de que un amplificador diferencial es muy versátil de manera que se puede utilizar tanto como amplificador inversor como no inversor. Dado un amplificador diferencial como el de la figura, la salida Vo sería...
Si V2=0, entonces Vo= G V1 y funcionaría como amplificador no inversor. Por otro lado si V1=0, entonces Vo= -G V2 y actuaría como un amplificador inversor. Y además, puede amplificar la diferencia.
Sin embargo, la verdadera razón para trabajar con amplificadores diferenciales proviene de la facilidad que poseen para trabajar con señales diferenciales frente a las de modo común, es decir, y como veremos ahora, nos va a permitir distinguir entre señal y ruido.
Veamos un ejemplo. Si pretendemos enviar una señal desde un circuito digital a un sistema informático remoto de forma asíncrona a través de un interfaz RS, se podría hacer utilizando un cable coaxial cuyo apantallamiento evitaría, teóricamente, la incidencia de ruido en la señal, como se ve en la figura adjunta.
Una estructura alternativa, más económica sería enviando la señal mediante dos hilos, de manera que a la entrada del sistema informático los dos hilos se conectaran a los terminales de un amplificador diferencial.
Está claro que la señal de salida sería Vo=G[(V1+Vr1)-(V2-Vr2)] en la cual aparecen unas tensiones Vr1 y Vr2 que representan el ruido añadido a la señal inicial. Si ambos hilos están íntimamente relacionados (hilo telefónico o par trenzado) se puede suponer que el ruido inducido es el mismo en ambos hilos (Vr1=Vr2), con lo cual la salida del amplificador será Vo=G(V1-V2) y si además, como es el caso, V2=0 por ser la toma de tierra, la salida del amplificador coincide con la señal emitida si G=1 o incluso la podemos obtener amplificada si G>1, libre de ruido en cualquier caso.
El esquema equivalente a lo indicado se ha dibujado justo encima de este párrafo y como se ve la tensión de entrada (VI) que alcanza al sistema informático sería VI = Vi ± (GND1-GND2).
En este caso, al utilizar un amplificador diferencial, y conectar los hilos a los terminales de entrada del amplificador diferencial que no están conectados a GND2, el amplificador diferencial elimina el ruido debido a la transmisión. En el caso en el que GND1 sea muy distinto de GND2 sería conveniente usar amplificadores de aislamiento.
Veamos algunas características del amplificador diferencial para ello estudiamos este circuito
Ya vimos en su momento que la resistencia de entrada Ri=R1+R3 pero debemos ver si este circuito es o no un amplificador diferencial. Anulamos primero V2 de manera que ahora
si anulamos ahora V1 tenemos que
sumando ambos términos la Vo total será...
Para que esta expresión representa una expresión del tipo diferencial de la forma Vo=G(V1-V2) debería cumplirse que
Una posible solución, para ser del tipo diferencial, sería que R2=R1 y que R3=R4 en cuyo caso obtendríamos que
que se trataría de un amplificador diferencial. Este amplificador se comportaría en la forma esperada si fuera
exactamente diferencial, sin embargo, las resistencias poseen una determinada tolerancia, por ello sus valores nominales no son exactamente los esperados. Con ello lo que resulta es que el amplificador diferencial se comporta como tal sólo parcialmente, por lo tanto habrá que añadir un término en modo común o algún parámetro que mida cómo de bueno es ese amplificador como amplificador diferencial, es decir tendríamos que utilizar un CMR del amplificador.
Vamos a ver cuál es el CMR de este circuito. Sabemos que está definido como
En el caso en que
se trata de un amplificador estrictamente diferencial. Pero en el caso general habrá que calcular la ganancia en modo común GCM. Para ello hacemos VD= 0 con lo que
Pero si VD=0 es porque V1=V2. Luego GCM es la ganancia del amplificador cuando V1=V2 quedando el circuito entonces de la forma
Si deseamos calcular el CMRR en dB habrá que hallar el logaritmo decimal multiplicar por 20.
Parece por tanto que el diseño de un amplificador diferencialpuede resultar una tarea fácil. Dado que queremos desechar el modo común utilizaríamos las resistencias que cumplan las igualdades R1=R3 y R2=R4. Después se trata, en principio, de calcular los valores de las resistencias R1 y R2 una vez conocidos los valores de la resistencia de entrada y la ganancia deseados. Sean estos, por ejemplo, Ri= 20 KΩ y GD=10.
Esto, que en principio parece fácil de lograr, no lo es ya que para que todo esto se cumpla debe ser R1 exactamente igual a R3 y R2 exactamente igual a R4. Pero las resistencias presentan errores que hacen que esta suposición sea muy difícil de alcanzar, sobre todo para resistencias que no tengan un valor económico muy alto. Por tanto la igualdad Vo= 10(V2- V1) no se obtiene de forma exacta sino que introducimos un error que lleva a una salida en modo común.
Cuanto mayor sea el error mayor será el término VCMGCM. En general, la mayor o menor bondad de un amplificador se da en términos de su CMRR. Si sólo se tiene modo diferencial sería GCM=0 lo que lleva a un CMRR infinito. Por tanto interesan valores altos de CMRR. Pero con el circuito que estamos estudiando solo se obtendrán valores de CMRR que, en el mejor de los casos es del orden de 104 , o lo que es lo mismo un CMRR de 80 dB. Esto es pequeño. Solo se puede hablar de un amplificador de calidad cuando se tienen un CMRR de unos 120 dB hacia arriba.
Vemos, por tanto, que el montaje de amplificador diferencial estudiado tiene una aplicación bastante limitada presentando los problemas de CMRR bajo, ganancia no modificable y resistencia de entrada no muy alta. Esto último se puede mejorar poniendo un seguidor a cada una de las entradas del diferencial. El circuito quedaría entonces
para lo que hemos utilizado tres amplificadores. Pero con este número de amplificadores se pueden onseguir mejores resultados cambiando la filosofía. Además el problema de la ganancia no modificable no es esoluble ya que necesitaríamos variar las resistencias por pares de una forma exacta y esto no es fácil ya que para variarlas tendríamos que hacer uso de potenciómetros. Incluso el método más recomendable de utilizar potenciómetros "en tándem" que modifican dos resistencias con un sólo mando, no da buenos resultados.
Vamos, por tanto a modificar totalmente el enfoque estudiando el circuito de dos etapas de la fig.
En este circuito se observa inmediatamente que se mejora la Ri con respecto a la del circuito anterior que era 2R1. Aquí es infinita.
Vamos a calcular la salida. Para ello podemos escribir
ya que la tensión V- es igual a V+=V1.
Además
y aplicando Kirchoff en el terminal - del primer amplificador
Con esto, la tensión de salida en el primer amplificador queda
Por otra parte
Aplicando Kirchoff en el terminal - del segundo amplificador
con lo que la salida queda
Para que esta salida sea diferencial debe cumplirse que el término que multiplica a V1 sea igual al que multiplica a V2. Se obtiene por tanto la condición
Esta configuración tiene la ventaja respecto de la anterior de que la ganancia se puede modificar exclusivamente con RG sin perturbar las características del amplificador como diferencial. En cuanto al CMRR, esta configuración presenta los mismos problemas que la anterior, alcanzándose valores similares
El circuito siguiente se denomina Amplificador diferencial de tres operacionales (de tres etapas)
Vamos a estudiar tres aspectos diferentes en este dispositivo: su resistencia interna, cómo de fácil es hacer variable la ganancia diferencial Gd y qué ocurre con su CMR.
La figura anterior se dividió en dos partes, de manera que la parte derecha se trata de un amplificador diferencial de una etapa, cuyo comportamiento ya ha sido ampliamente tratado.
Veamos, pues, el resto.
Si somos capaces de calcular Va y Vb, podemos aplicar ese resultado a la segunda parte. Si aplicamos el principio de superposición, suponemos primero que V2=0, en ese caso nos queda
Suponemos ahora que V1=0
Sumando las dos contribuciones obtenemos...
Aplicando estos valores al amplificador diferencial de una etapa que tenemos en el lado derecho obtenemos Vo
esta sería la expresión general. Una condición ideal sería cuando se cumpliera que R2=R'2 y además R3=R'3, en ese caso tendríamos:
Sustituyendo las expresiones anteriores de Va y Vb
ecuación que representa el caso más genérico. Si sustituimos para obtener Vo
observamos que esta expresión corresponde a un amplificador diferencial a pesar de haber supuesto condiciones únicamente en su segunda parte. El hecho de que R1 y R'1 sean iguales o no, no influye en el carácter diferencial del dispositivo. Ahora bien, se suele hacer que R1 sea igual a R'1, y en ese caso la expresión toma la forma
de donde obtenemos la expresión de la ganancia diferencial
Si analizamos con detenimiento esta expresión observamos que también esta ecuación se puede dividir en dos partes, debidas cada una de ellas a las partes en que se dividió el circuito anteriormente. Así, la ganancia diferencial total se obtendría como el producto: Gd= Gd1 Gd2. Por ello, Gd2 será debida a la parte del amplificador diferencial de una etapa (parte derecha de la figura) y Gd1 será la ganancia debido a lo que queda del circuito
La ganancia general Gd sería variable si hacemos variable R1, R'1 o RG. El caso más sencillo sería haciendo variable RG, a medida que disminuye esta resistencia mayor es la ganancia diferencial.
Para calcular el CMR sustituimos en su expresión
no sabemos qué expresión representa al GCM. Por ello, colocamos a la entrada de los terminales una tensión en modo común VCM
dado que en los extremos de RG la tensión es la misma (VCM), por ello la intensidad que la atraviesa es nula y con ello se deduce que tanto Va como Vb poseen la misma tensión VCM. Con ello lo que estamos viendo es que la primera etapa posee una ganancia unidad y por tanto GCM=GCM2. Sustituyendo...
obtenemos el CMR como producto de la ganancia diferencial de la primera etapa por el CMR de la segunda. Para un valor dado de Gd, la ganancia puede ser debida sólo a la primera parte Gd1, sólo a la segunda Gd2, o compartida entre ambas. Como nos interesa que el CMR sea grande es interesante darle la mayor ganancia posible (si no toda la ganancia) a la primera etapa Gd1, para que el factor que multiplica al CMR2 sea mayor que la unidad.
Vamos a estudiar este circuito desde el punto de vista de los valores de Ri y CMR, la variabilidad de la ganancia Gd para compararlos con los de otros circuitos estudiados y ver si este circuito es más adecuado.
La resistencia de entrada es infinita.
La variación de la ganancia se puede hacer de forma independiente en cada una de las etapas, pero no es conveniente hacerlo en la segunda ya que de nuevo tendríamos el problema ya planteado en el estudio de esa etapa realizado anteriormente: al estar las resistencias emparejadas, el hecho de variar una lleva a variar de igual forma su pareja lo cual es difícil de ajustar. En la primera etapa ese problema no existe y se puede variar R1 y RG. Sin embargo, es más útil y corriente variar esta última que se encuentra sola. Por último, el comportamiento del CMR va a ser substancialmente mejor que en los otros circuitos estudiados siempre que se cumplan algunas condiciones.
Sabemos que
Para que el CMR sea mayor que el CMR2 tiene que ser la GD1 alto. Si el GD1 = 1 es CMR = CMR2 y no hemos ganado nada con este circuito. Para que se pueda hablar de una mejora substancial de este circuito frente al otro tendría que ser GD1 del orden de 100 -500. Por tanto para unos requerimientos determinados de la ganancia total del circuito y dado que GD= GD1. GD2 siempre será mejor que la ganancia de la primera etapa sea la más alta. Por ej. si queremos una GD de 100, lo podemos obtener mediante muchas combinaciones de GD1 y GD2, por ejemplo GD1= 1 y GD2=100, o GD1= 10 y GD2=10, o GD1= 100 y GD2=1 etc. De todas ellas, la más recomendable sería aquella en que GD2=1 y GD= GD1 ya que esto dará un mejor CMR.
Además, esto tiene también un efecto positivo sobre la influencia del offset. Para ver en qué forma influye vamos a considerar el circuito que estudiamos como dos etapas amplificadoras en las que los errores de offset están representados por dos fuentes externas a ellas. Cada uno de los triángulos es un esquema de cada una de las etapas con varios amplificadores. Para ver el efecto que produce el offset anulamos las entradas y obtenemos la salida.
La salida de la primera etapa es VIO1. GD1 y la del segundo es (VIO1. GD1 + VIO2). GD2 que se puede dividir en dos términos distintos:
Por tanto el error debido al offset tiene dos términos distintos. En el primero se encuentra el producto de la ganancia de las dos etapas, y por tanto es indiferente cuál de las dos sea mayor para que el error sea menor. Sin embargo, en el segundo aparece sólo GD2. Interesa, por tanto para que el error producido por el offset sea pequeño, que GD2 sea lo menor posible por lo que la ganancia del circuito total conviene que este condentrada en GD1. Una situación óptima será GD2=1 y GD= GD1. Así tendremos un CMR alto y un error de offset pequeño.
Normalmente, este tipo de circuitos no se montan con elementos discretos, sino que los fabricantes proporcionan una de las etapas o el circuito completo ya integrados. Hay varias alternativas en cuanto a las estructuras proporcionadas por el fabricante. La más sencilla es una variante del circuito ya visto:
Colocando una resistencia RG entre RG1 y RG2, uniendo la salida SENSE con la VOUT y la VREF a masa se tiene el circuito que acabamos de estudiar.
El utilizar un circuito ya integrado tiene como ventaja principal que la precisión de las resistencias es mucho mejor más comparativamente que en el valor nominal propiamente dicho.
Se consigue por tanto un CMR muy alto. Estructuras como esta consiguen un CMRR de aproximadamente 130 dB. Por otra parte, mediante la RG colocada se puede variar la ganancia del amplificador según las necesidades que tengamos. Esto es muy útil ya que normalmente el amplificador está conectado a la salida de un sensor que, según lo que estemos midiendo puede dar salidas dentro de un rango muy distinto. Como la ganancia de esta etapa es :
donde R1 tiene un valor conocido que proporciona el fabricante. Se puede por tanto conocer el valor que debe tener RG para una ganancia dada.
Dentro del campo de la adquisición de datos también se pueden dar casos como el siguiente
en el cual disponemos de tres sensores diferentes y un único voltímetro de salida, cuya variación ha sido establecida en el rango 0 - 10 V. En un momento dado sólo se quiere medir a través de un único sensor, con lo cual se necesita un conmutador que seleccione la entrada deseada. Con cada elección posible de un sensor habrá que tener en cuenta sus propias características diferentes y por tanto su ganancia frente a los otros sensores posibles. Con todo esto llegamos a que el selector debe elegir, no sólo el sensor deseado, sino también su ganancia correspondiente. Esto es posible mediante el diseño que aparece en la figura siguiente, en donde disponemos de diferentes resistencias RG de manera que asociamos el valor adecuado de la resistencia RG a cada caso concreto. En este tipo de montaje se supone que los contactos, una vez establecidos, no presentan resistencia alguna, lo cual es fácilmente asequible.
En nuestro ejemplo sería necesario un conmutador 2x4, cuyo significado es un conmutador de dos secciones (una elige el sensor y la otra la resistencia RG correspondiente) con hasta cuatro posiciones diferentes de contacto (en nuestro caso sólo sería necesario tres contactos).
Una tercera aplicación sería al utilizar varios sensores de entrada y almacenar la información recibida a lo largo del tiempo. Para ello, se conmutaría al sensor 1, almacenado su medida para conmutar posteriormente al sensor 2 y almacenar también su valor, conmutar al sensor 3 y así sucesivamente, volviendo de nuevo al sensor 1, al 2, etc. En este caso sería conveniente eliminar al operador, de manera que no fuera necesaria su actuación, con lo cual nos llevaría a una actuación automatizada.
El primer aspecto a tener en cuenta es el referido a cada cuánto tiempo se pasa de un sensor al siguiente. Naturalmente se trata de un aspecto importante ya que no se resuelve de igual forma los casos en los cuales se produce una conmutación por segundo (frecuencia de conmutación de 1 Hz), como ocurre en medidas de J.I.Escudero, M.Parada, F.Simón I TMM 2-20pH o radiación solar, que aquellos otros que requieren 100.000 conmutaciones por segundo, como se puede dar en el caso de estudios de transitorios.
Lo primero que tenemos que establecer es precisamente qué elementos son necesarios para poder obtener nuestra frecuencia de conmutación. El primer paso será pasar de conmutadores manuales a automáticos y comenzamos hablando de relés.
Para mas información acerca del tema visitar la siguiente pagina web :http://www.dte.us.es/ing_inf/ins_elec/temario/Tema%202.%20Amplificadores%20de%20Instrumentacion.pdf



























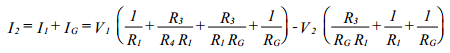




































0 comentarios:
Publicar un comentario