PUENTES DE MEDICIÓN
Puente de Corriente Alterna
En principio, un puente de corriente
alterna consta de cuatro ramas cada una de las cuales tiene cierta
impedancia, una fuente de voltaje AC y un detector de cero, interconectados de
la manera mostrada en la Figura
Analizando
este circuito podemos concluir que, en forma similar al puente de Wheatstone,
cuando no hay circulación de corriente por el detector de cero se cumple la
relación :
Puente de Wheatstone.
El puente Wheatstone es un circuito muy interesante y se
utiliza para medir el valor de componentes pasivos como las resistencias.
Este circuito consiste en tres
resistencias conocidas y una resistencia desconocida, conectadas entre sí en
forma de diamante. Se aplica una corriente continua a través de dos puntos
opuestos del diamante y se conecta un galvanómetro a los otros dos puntos.
Cuando todas las resistencias se nivelan, las corrientes que fluyen por los dos
brazos del circuito se igualan, lo que elimina el flujo de corriente, el puente
puede ajustarse a cualquier valor de la resistencia desconocida, que se calcula
a partir los valores de las otras resistencias. Se utilizan puentes de este
tipo para medir la inductancia y la capacitancia delos componentes de
circuitos. Para ello se sustituyen las resistencias por inductancias y
capacitancias conocidas. Los puentes de este tipo suelen denominarse puentes de
corriente alterna, porque se utilizan fuentes de corriente alterna en lugar de
corriente continua.
Circuito Equivalente
El
puente de Wheatstone se muestra en la siguiente figura y está
constituido por cuatro resistencias R1, R2, R3 y R4, de las cuales una de ellas es desconocida y su valor
debe determinarse
Formula Matemática
El puente Wheatstone tiene cuatro ramas resistivas, una
fuente de f.e.m (una
batería ) y un detector de cero (el galvanómetro). Para determinar la
incógnita, el puente debe estar balanceado y ello se logra haciendo que el
galvanómetro mida 0 V, de forma que no haya paso de corriente por él. Debido a
esto se cumple que:
Al
lograr el equilibrio, la corriente del galvanómetro es 0, entonces:
Donde
Rx es
R4, combinando las ecuaciones (7.1), (7.2) y (7.3) se obtiene:
Resolviendo:
Expresando
Rx en
términos de las resistencias restantes:
R3 se denomina Rama Patrón y R2 y R1
Ramas de Relación.
El puente de Wheatstone se
emplea en mediciones de precisión de resistencias desde 1 hasta varios M Ohm.
Puente de kelvin
El puente kelvin es una modificación del Wheatstone que
utiliza como elementos de comparación
resistencias muy pequeñas inferiores a 1 Ω
Considérese
el circuito puente de la siguiente figura, donde Ry representa
la resistencia del alambre de conexión de R3 a Rx
. Son posibles dos conexiones del galvanómetro, en el punto m ò en el punto n.
Cuando el galvanómetro se conecta en el punto m, la resistencia Ry
del alambre de conexión se suma a la desconocida Rx,
resultando una indicación por arriba de Rx
Considérese
el circuito puente de la siguiente figura, donde Ry representa
la resistencia del alambre de conexión de R3 a Rx
. Son posibles dos conexiones del galvanómetro, en el punto m ò en el punto n.
Cuando el galvanómetro se conecta en el punto m, la resistencia Ry
del alambre de conexión se suma a la desconocida Rx,
resultando una indicación por arriba de Rx
La
ecuación de equilibrio para el puente da:
Remplazando
la ecuación 2 en 1 tenemos
El término doble se debe a que el
circuito tiene un segundo juego de ramas de relación. Se utiliza para medir
resistencias menores a 1[Ω].
Las resistencias Rx
y Rp son
resistencias de 4 terminales, construcción que se emplea para Shunt
y patrones de resistencias. La resistencia de 4 terminales tiene 2 pares de
bornes, es decir dos bornes de tensión (bornes superiores) y dos bornes de
corriente (bornes inferiores).
CIRCUITO EQUIVALENTE
FORMULA MATEMATICA
El
equilibrio se cumple:
Resolviendo
la ecuación:
La
expresión para Rx nos queda
Puente de Schering
Este es un tipo de puente que está
concebido para realización de medidas en altas tensiones, su objetico se dirige
principalmente hacia la determinación del factor de perdida, y no tanto en la
determinación de capacidades de elementos aislantes de alta tensión en equipos
ya fabricados o instalados así como para la realización análisis de materiales
sometidos a altas tensiones
Su constitución puede verse en la
siguiente figura. En ella el elemento en prueba es el correspondiente a Cx y
ᵹx. Cn es
un condensador conocido de aire o vacío, por tanto sin perdidas, y adecuado
para trabajar a alta tensión de ensayo
Zpr es un elemento de protección para
limitar la corriente de cortocircuito en caso de fallo del aislante de algunos
de los elementos anteriores citados
CIRCUITO EQUIVALENTE
El balance de ángulos exige que el ánulo
Ѱ de esta rama y el ángulo ϕ del elemento incógnita deban sumas exactamente
-90°. Las ecuaciones que igualan los productos de rama opuestas proporcionan
las siguientes condiciones de equilibrio
Y
Puente de Sauty
Es un
puente que permite medir capacitores permitiendo establecer el circuito
equivalente serie. Dos ramas adyacentes son resistencias puras y las otras dos
del mismo carácter reactivo.
Ecuaciones
de equilibrio
Remplazando
en la ecuación anterior
Puente de Anderson
Una forma modificada de puente de Maxwell
utilizada para la medida de inductancias
en términos de capacitancia y resistencia. Como se muestra en la siguiente
figura el puente posee una resistencia adicional R5. Las condiciones de
equilibrio (que son independientes de la frecuencia)
ECUACIÓN MATEMÁTICA
CIRCUITO EQUIVALENTE
Puente de Maxwell
El puente de Maxwell compara una
inductancia con una capacitor. Este puente es muy adecuado para medir
inductancia en función de la capacidad, dado que los capacitores ordinarios
están mucho mas cerca de ser patrones de reactancia sin perdidas, que los inductores.
Además la ecuación de equilibrio del
puente de Maxwell para la componente inductiva es independiente de las perdidas
asociadas con la inductancia y también de la frecuencia con que se mide.
Este puente es conveniente para la
medición de inductancias de cualquier magnitud, siempre que el Q de la misma no
sea muy elevado a la frecuencia de medición.
Circuito Equivalente
El puente se ilustra en el siguiente
circuito y se usa para la medida de
inductancias (en función de un condensador conocido) o capacidades (en función
de una inductancia conocida).
Formula Matemática
Tenemos:
L/C = R4R2=R1R3
Despejamos y obtenemos
Puente de Hay
El circuito puente Hay se utiliza
generalmente para la medida de inductancias en términos de capacitancia,
resistencia y frecuencia. Se diferencia del puente de Maxwell en que el
condensador se dispone en serie con su resistencia asociada.
Formula matemática
Circuito Equivalente
A primera vista este puente no difiere
demasiado de su equivalente de Maxwell, salvo
que en esta ocasión el capacitor C1 se conecta en serie con la
resistencia R1, por lo tanto para
ángulos de fase grandes la resistencia
R1 debe tener un valor muy bajo. Es esta pequeña diferencia constructiva la que permite su
utilización para la medición de bobinas de Q alto (Q>10).
Puente de Wien
Un
circuito puente de CA, en el que una rama consta de una resistencia y una
capacitancia en serie, y la contigua de una resistencia y una capacitancia en
paralelo, siendo las dos ramas restantes puramente resistivas.
Formula matemática
Este puente se usa para medida de
capacitancias en términos de resistencia y frecuencia. En el equilibrio, se
aplican las siguientes relaciones:
Que
dan las siguientes expresiones para C1 y C2:
Circuito Equivalente
Usa el mismo esquema que el puente de
corriente alterna pero el capacitor incógnita (por ejemplo C1) es un capacitor
imperfecto con perdidas por lo que para poder equilibrar el puente hay que
agregar una resistencia variable a la otra rama capacitiva.
















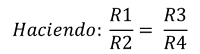


























Excelente contenido!
ResponderEliminar